II. Mysterium Cosmographicum
III. Biographie - rencontre avec Tycho Brahe
Jusqu'où peut-on parler d'héliocentrisme ?
Dès 1595, Kepler rédigea son premier ouvrage, le Mysterium Cosmographicum, qu'il publia l'année suivante grâce au concours de Maestlin. Sa vocation d'astronome s'y révèle, en même temps que ses motivations profondes. Kepler le déclare expressément : au moment où il écrit, il y a six ans déjà qu'il est copernicien. Depuis lors, sa conviction n'a fait que croître, mais avec une pensée qui est nouvelle, à savoir qu'un système qui rend raison des phénomènes observés d'une manière aussi satisfaisante et grâce à une explication unique, le mouvement de la Terre, n'est pas seulement une heureuse fiction. Il doit être vrai, parce que ce n'est qu'accidentellement que des conséquences vraies découlent de prémisses erronées. Mais, si les avantages « mathématiques » du système de Copernic sont si grands qu'ils débouchent sur une vérité physique, il faut à la fois démontrer le plus rigoureusement possible leur existence et leur qualité et définir les traits de cette vérité qui les soutient.
Pour attirer des élèves que l’austérité de l’astronomie rebute, Kepler décide de traiter de questions astrologiques. Très exactement le 19 juillet 1595, comme il le notera lui-même dans son souci maniaque de précision numérique, alors que, désirant montrer à ses élèves comment les grandes conjonctions sautent par-dessus huit signes du zodiaque, il dessinait au tableau une longe suite de triangles inscrits dans un cercle, une idée le frappa avec tant de force qu’il pensa tenir la clef des secrets géométriques de la création : « Jamais je ne pourrai exprimer par des mots quelle joie m’a donné cette découverte » écrira-t-il dans sa préface à l’édition de 1596 du Mysterium Cosmographicum.
L’enseignement qu’il a reçu de Michael Maestlin a fait de lui un copernicien convaincu et il a déjà dressé une liste des avantages mathématiques que présentait le système de Copernic sur celui de Ptolémée, en bonne place figurait ce lien, non encore mathématiquement formulé mais quantativement évident entre les dimensions des orbes et les durées des révolutions. Pourquoi ce lien ? Mais aussi, pourquoi ces orbes étaient-ils au nombre de six et pourquoi avaient-ils entre eux ces distances ?
Première question : n’y aurait-il pas entre les rayons des orbes successifs un rapport simple que des nombres entiers exprimeraient, ou bien un tel rapport n’existerait-il pas entre leurs différences ? Recherche vaine. Kepler consacrera beaucoup de temps à ce travail comme à un jeu puisque nulle irrégularité n’apparaissait ni dans les proportions des orbes ni dans leurs différences.
N’ayant donc rien obtenu par cette voie, Kepler en explorera une autre tout aussi vainement : il intercalera entre Jupiter et Mars ainsi qu’entre Vénus et Mercure deux petites planètes que leur petitesse nous empêcherait de voir ; en leur attribuant de plus une durée de révolution, il pensait produire une certaine régularité dans les rapports entre les orbes. Toutefois, dès l’abord le procédé le choque, car il ne peut faire de conjectures raisonnables sur la noblesse d’aucun nombre qui limiterait le nombre de planète entre le Soleil et la sphère des fixes. De plus, il lui semble préférable de supposer que Dieu a établi son plan du monde sur des rapports géométriques, plutôt que sur des rapports numériques, puisque les nombres sont postérieurs à la création du monde.
L’événement du 19 juillet 1595 lui revient alors en mémoire. Kepler inscrivait dans un même cercle une multitude de triangles. Les points où se coupaient mutuellement les côtés des triangles esquissèrent la forme d’un cercle deux fois plus petit que le cercle initial. La proportion entre l’un et l’autre paraissait à l’œil presque semblable à celle qui existe entre l’orbe de Saturne et celui de Jupiter, et, de plus, le triangle étant la première des figures, tout comme Saturne et Jupiter sont alors les premières planètes, c’est l’illumination et une nouvelle fausse piste.
Il tente de déterminer la distance entre Jupiter et Mars à l’aide du carré ; celle entre Mars et la Terre à l’aide du pentagone ; celle entre la terre et Vénus, à l’aide de l’hexagone et celle entre Vénus et Mercure, à l’aide de l’heptagone.
Certain désormais de détenir la clef du secret du monde, Kepler analyse les raisons de ce dernier échec, à suivre l’ordre des figures, il ne parviendra jamais au Soleil et n’obtiendra jamais la raison du nombre des orbes : pourquoi six plutôt que vingt ou cent ? Il partira donc de la Terre et, passant de la géométrie plane à la géométrie dans l’espace plus apte à rendre compte de la structure du monde, il n’utilisera, pour combler les cinq espaces qui séparent les six orbes, que les cinq polyèdres réguliers, dont Euclide a montré qu’il ne pouvait en exister plus de cinq et qui, du temps de Platon étaient déjà associés aux éléments du monde.
Pour Kepler, les cinq polyèdres réguliers structurent le monde : entre la sphère de Saturne et celle de Jupiter, il insère le cube ; puis entre celle de Jupiter et celle de Mars, le tétraèdre ; puis, entre celle de Mars et le Grand Orbe de la Terre, le dodécaèdre, puis entre la sphère de la Terre et celle de Vénus, l’icosaèdre et entre celle de Vénus et celle de Mercure, l’octaèdre.
Le miracle réside dans l’accord presque parfait entre les rayons successifs des sphères inscrites et circonscrites aux polyèdres réguliers pris dans cet ordre et les distances relatives des planètes au Soleil dans le système de Copernic.
Sans doute se refusait-il à se satisfaire, comme Rheticus, l'ami de Copernic, de la perfection du nombre six, qui caractérise le nouveau monde planétaire dans lequel la Lune, satellite de la Terre, n'est plus à compter. Mais il mettait en avant l'image de la Sainte Trinité qu'il croyait voir dans le monde immobile (le Soleil, l'espace, les étoiles fixes) pour justifier sa recherche des lois du monde mobile comme reflets des perfections divines, comme nécessités inscrites dans la Création même.
Aussi ne reste-t-il rien de cet emboîtement de sphères et de polyèdres réguliers qui constitue la solution dernière du Mysterium Cosmographicum. Même en donnant une épaisseur à ces corps inscrits les uns dans les autres, afin de pouvoir « loger » les orbites planétaires, Kepler n'est pas parvenu à assumer de manière convaincante la confrontation de son édifice géométrique avec les dimensions des orbites calculées sur les données de l'observation. A fortiori, il ne reste rien de la démonstration que Dieu n'a pu créer que six planètes du fait qu'il n'y a que cinq polyèdres réguliers.
II. Mysterium Cosmographicum
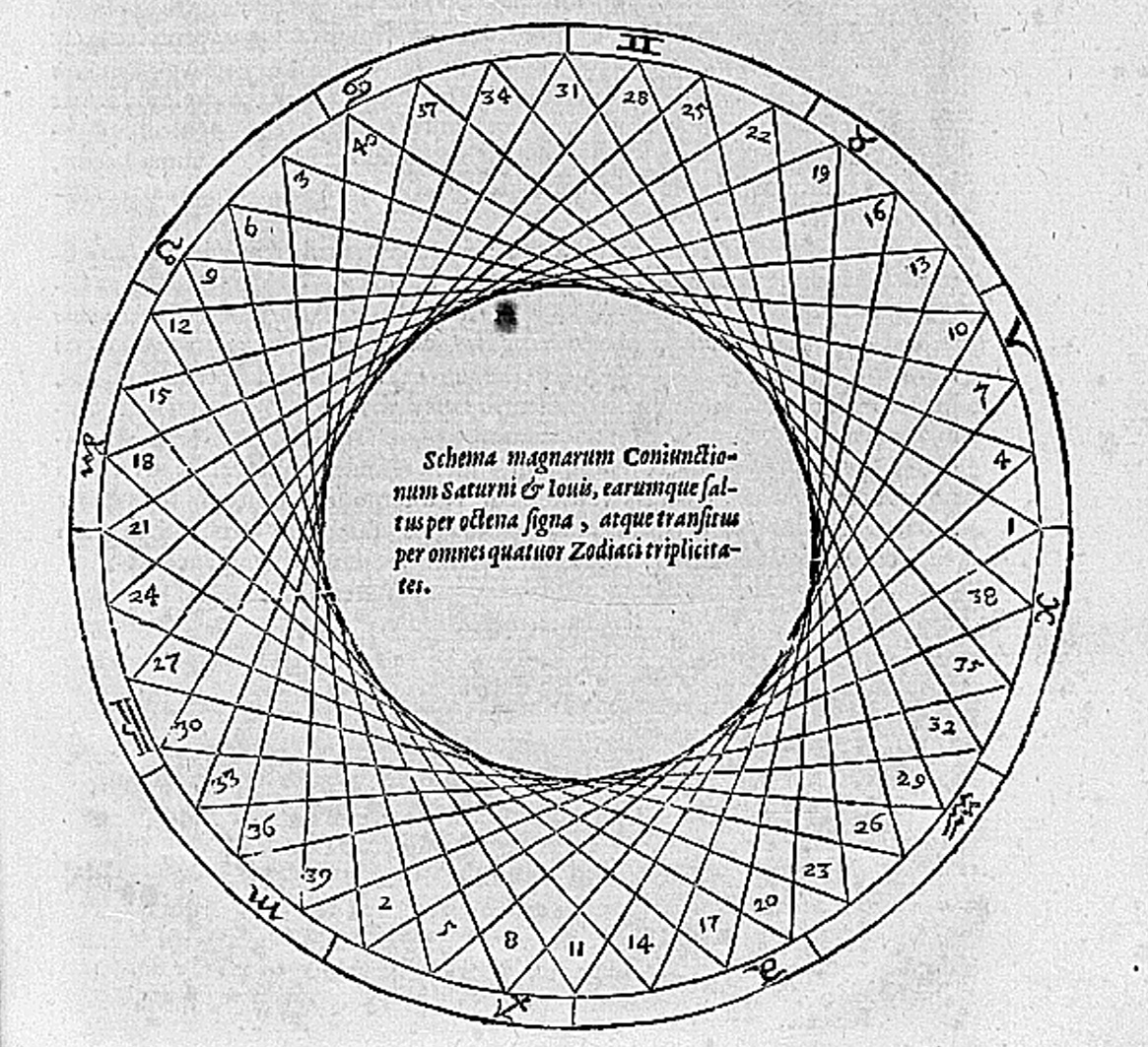
Schéma de l'expérience du 19 juillet 1595

Les cinq polyèdres réguliers