III. Biographie - rencontre avec Tycho Brahe
IV. Astronomia Nova
Jusqu'où peut-on parler d'héliocentrisme ?
Dix années séparent la tentative précédente du grand ouvrage qui ouvre bien, conformément à son titre, Astronomia Nova, l'ère d'une astronomie nouvelle. Encore faudra-t-il trois ans de plus pour qu'il soit imprimé, en 1609.
L'opposition de Brahe a eu en effet une heureuse influence, celle de déterminer Kepler à s'attacher davantage à un examen précis et à combiner du mieux possible les arguments a priori et les arguments a posteriori.
C'est en reprenant les travaux de Brahe sur Mars, et en constatant un écart de 8´ entre les positions observées et les positions calculées avec le système des combinaisons de mouvements circulaires que Kepler fut amené à entreprendre d'abord une révision de l'orbite terrestre. Brahe avait remarqué une excentricité dans la trajectoire de Mars, considérée comme une anomalie à une époque où l’on pensait encore que les planètes décrivaient des cercles, figure parfaite.
La première loi précise la nature des orbites : les planètes décrivent des ellipses dont le Soleil occupe l’un des foyers.
Jusqu'alors, on n'avait considéré que le cercle comme trajectoire possible des corps célestes. Ce sont les observations précises de Brahe qui ont permis de revenir sur ce postulat. L'ellipticité des orbites des planètes est très faible. La différence entre le cercle et l'orbite de la Terre est infime : si on veut la représenter sur une feuille de papier, la différence entre le cercle et l'ellipse tient dans l'épaisseur du trait de crayon. Heureusement le Soleil n'est pas au centre de l'ellipse, mais au foyer qui est décentré.
La deuxième loi de Kepler précise le mode de parcours des orbites : les aires décrites par le rayon vecteur planète-Soleil sont proportionnelles aux temps employés pour les décrire.
La signification de cette loi est claire : les planètes ne tournent pas avec une vitesse uniforme ; elles vont plus vite quand elles sont près du Soleil et plus lentement quand elles en sont loin. Cela est particulièrement observable pour les comètes dont les orbites sont, contrairement à celles des planètes, très excentriques.
Examinons la découverte de ces deux premières lois. Le problème était le suivant : de la Terre, nous apercevons le Soleil et les planètes dans certaines directions par rapport aux étoiles ; ces directions varient de jour en jour, à mesure que la Terre décrit une courbe inconnue autour du Soleil et que les planètes décrivent aussi des courbes inconnues autour de lui ; il fallait donc trouver la trajectoire de la Terre. On voit ici l’importance dans les travaux de Kepler de l’héliocentrisme de Copernic.
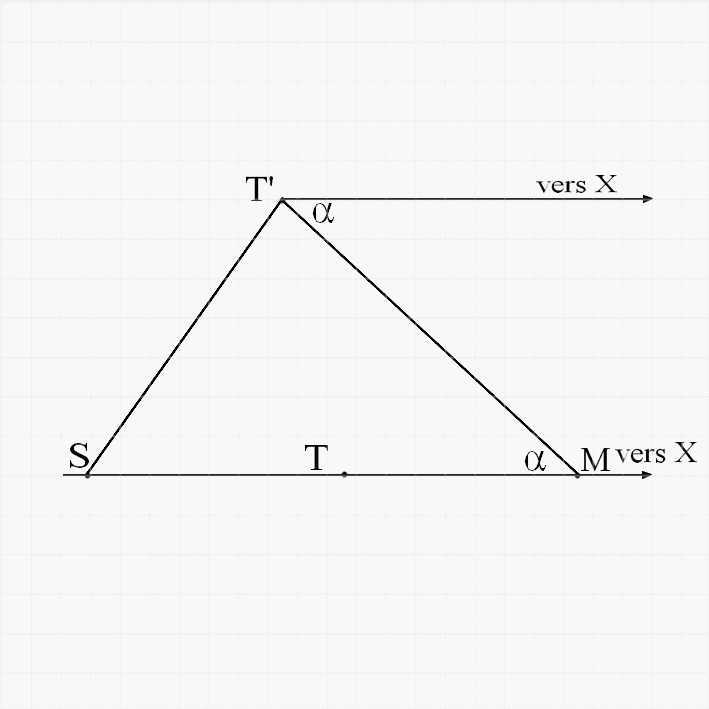
Quand Mars et le Soleil sont en opposition, les points S, T et M sont alignés : soit X une étoile qui matérialise la direction de cette droite, l’étoile étant supposé fixe. Mars accomplit son orbite en six cent quatre-vingt-sept jours et revient en M, la base SM se retrouve alors en grandeur et en direction, SMX sont à nouveau alignés, mais au bout de ce temps la Terre occupe une position T’, l’observation de Mars à cette époque fait connaître les angles indiqués en T’.On peut construire le triangle SMT’, avec un côté SM arbitraire. Après six cent quatre-vingt-sept jours encore, on pourra construire avec le même côté SM une nouvelle position T’’ de la Terre et ainsi de suite. Avec une série de n observations, on aurait n positions correctes de la Terre par rapport à la base fixe SM et l’on pourrait chercher empiriquement quelle orbite peut contenir ces points n.
Grâce aux observations de Brahe, Kepler parvint à construire une orbite correcte pour la Terre : un cercle de centre C excentré par rapport au Soleil de 0,018 (le rayon du cercle étant pris comme unité)
Ce résultat est excellent et ne doit pas étonner, car l’ellipse terrestre diffère peu d’un cercle.
Cette brillante découverte fut le tremplin des deux premières lois. Possédant une trajectoire correcte de la Terre, Kepler s’attaque aussitôt à son mode de parcours et, à travers deux erreurs qui se compensent, trouve la loi des aires. La deuxième loi fut donc établie avant la première, et concerna d’abord le cercle excentré et non l’ellipse. Lorsque plus tard Kepler découvrira l’orbite elliptique de Mars, il lui appliquera la loi des aires, constatera qu’elle donne des positions correctes et la tiendra alors pour établie.
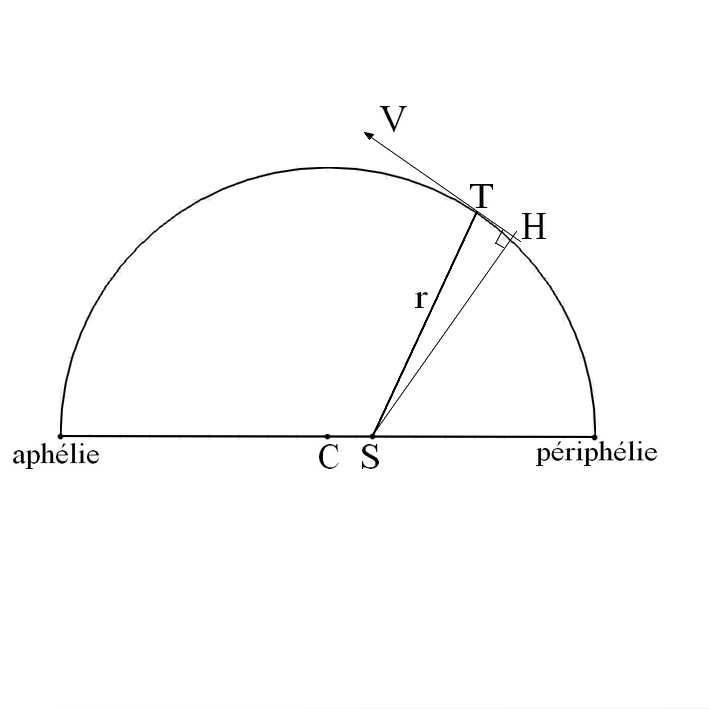
Pour lui, la force motrice réside dans le Soleil ; elle est de nature magnétique et provient de sa rotation sur lui-même. La force s’exerce tangentiellement à la trajectoire, la planète s’arrêterait si une force ne la poussait pas en permanence. Si r est la distance du Soleil à la planète, la force motrice varie en raison inverse de r et la vitesse de l’astre aussi pense Kepler. Or la vitesse varie en raison inverse de SH et non de ST. Mais quand la planète passe en A ou en P (apsides), ST et SH se confondent. Or, Kepler se borna précisément à vérifier la loi des vitesses aux apsides, l’erreur ne lui apparut donc pas.
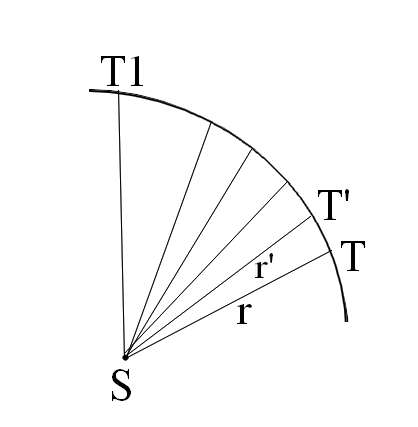
Mais une seconde faute vint annuler l’effet de la première. Croyant la vitesse en T inversement proportionnelle à ST, Kepler en déduit légitimement que le temps mis à parcourir un arc très court TT4 est proportionnel à ST. Le parcours d’un arc plus long TT1 exigera un temps proportionnel à la somme des rayons (ST+ST’+…+ST1). Or, Kepler remplace la somme des rayons par l’aire du secteur. Remplacer une longueur par une surface est une faute grossière, Kepler ne l’ignore pas et le reconnaît. Mais, comme la loi des aires s’avère conforme aux phénomènes, il la conserve, bien qu’il ne puisse mieux la justifier.
Possédant une orbite terrestre excellente et la loi véritable de son parcours, Kepler reprend l’étude de Mars. Sa méthode est de calcul pur, mais pour simplifier, la voici sous forme graphique. Considérons deux observations de Mars à six cent quatre-vingt-sept jours d’intervalle.
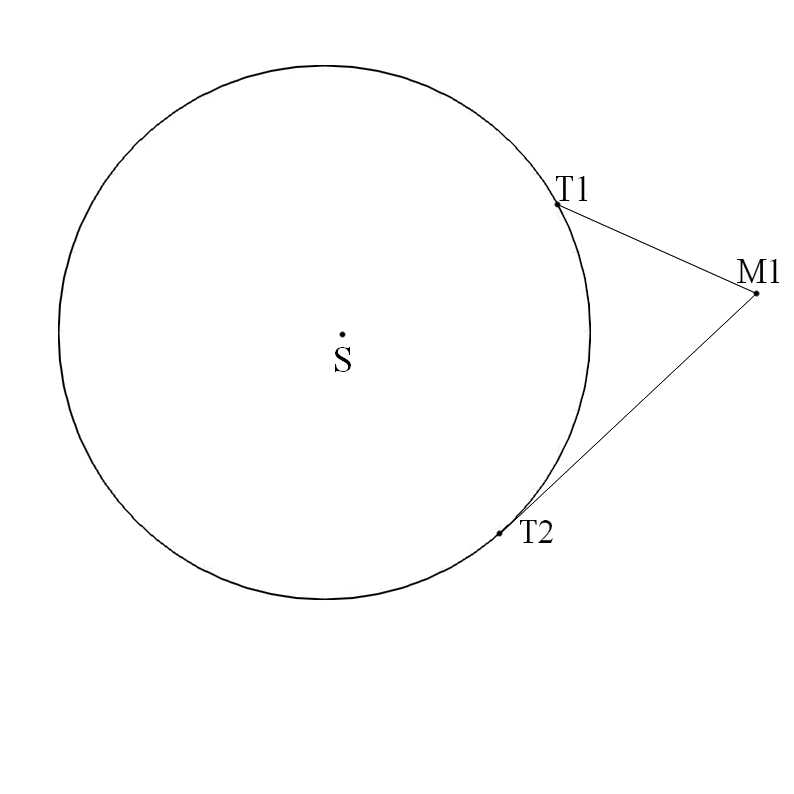
Mars a repris la même position M1 par rapport au système solaire, mais la Terre occupe deux positions distinctes T1 et T2 qu’il est désormais facile de situer.
Les visées de Mars à chaque date se coupent au point M1 cherché. On peut recommencer à une date différente puis à nouveau six cent quatre-vingt-sept jours plus tard. On obtiendra alors un point M2. En recommençant n fois cette opération, on obtient n points, M1, M2, …, Mn, qui dessinent la trajectoire de Mars. Kepler essaie d’abord un cercle. Avec des points au voisinage des apsides, il détermine les éléments d’un excentrique et calcule l’écart des autres positions par rapport à ce cercle. Il trouve en certains points des écarts de huit minutes d’arc, alors que la précision des observations est de deux minutes, et commence à suspecter le cercle. Kepler conçoit que la trajectoire doit être ovale et il la voit d’abord en forme d’œuf, pointue vers le périhélie. Mais, dans cet ovale la méthode des aires est une application difficile. Il se tourne donc vers l’ellipse. Il remplace l’ovale par une ellipse assez aplatie, dont le Soleil n’occupe pas l’un des foyers. Ce nouvel essai lui redonne des erreurs de même grandeur mais de signe contraire, l’orbite vraie se situe entre le cercle apsidal et l’ellipse. L’écart est précisément la moitié de la lunule et Kepler voit qu’il correspond à une ellipse dont le Soleil serait un foyer.
Le plus redoutable des obstacles est psychologique. Kepler détaille dans ce livre sa résistance inconsciente à toute solution qui ne fût pas circulaire et uniforme pour les orbites planétaires. Il nous raconte même ce moment émouvant et pathétique où l'évidence s'impose à lui, où il découvre qu'elles sont non seulement elliptiques mais également non uniformes. Il s'exclame alors : « J'ai nettoyé les écuries d'Augias ! ».
III. Biographie - rencontre avec Tycho Brahe
IV. Astronomia Nova

Schémas des travaux de Tycho Brahe sur Mars
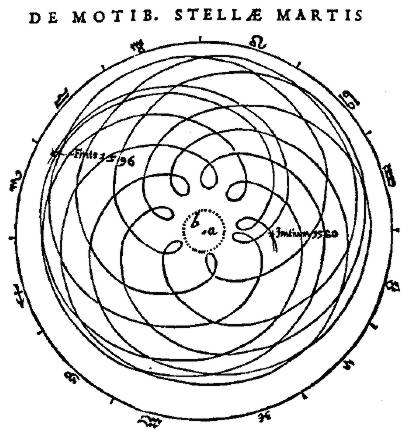
Mouvements rétrogrades de Mars